In 2020 a group from the School of Agricultural, Forest and Food Sciences at Bern University of Applied Sciences in Switzerland had, as part of their STEC objective, the aim of improving shallow landslide modelling by considering the mechanical effect of vegetation. For this objective we completed two major tasks: improving the model SlideforMAP and extending calibration data for poplar (Populus sp.) with fieldwork in New Zealand.
Modelling
SlideforMap (SfM) functions as a probabilistic, limit equilibrium, method-based model with an emphasis on vegetation effects. The probabilistic approach enables the model to encompass more uncertainty in the parameterisation, as most environments are highly heterogeneous. Also, the influence of trees can be spatially differentiated based on the actual location and dimensions of the trees. The complete methodology of SfM is outlined in Figure 1.
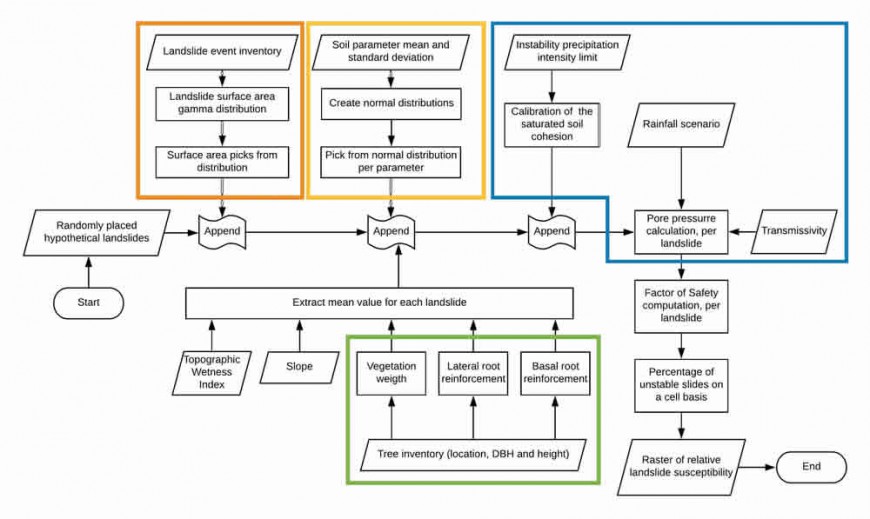
Figure 1. The workflow used in SlideforMap. Separate sections are outlined in different colours: orange is the landslide surface area computation; yellow is the definition of the soil parameters; green is the vegetation module; and blue is the hydrology module.
The probabilistic approach involves creating a large number of hypothetical landslides (HLs) at random locations within a study area. These HLs are provided with a surface area from the landslide surface area distribution, as described in Malamud et al. 2004. An inventory of past landslides is required to calibrate this distribution. Soil parameters are allotted to the HLs using normal distributions.
Hydrological computations are necessary to parameterise the degree of saturation of a potential shallow landslide. The hydrology input to the model makes use of a TOPMODEL approach (Montgomery & Dietrich 1994). This assumes a steady, stationary, groundwater flow. The saturation at each point in the landscape is then a function of the following factors: specific catchment, slope angle, transmissivity of the soil, and precipitation.
The vegetation module makes use of single tree detection. The position and dimensions of the trees can be estimated by the difference between a digital surface model and a digital terrain model, but other methods can also be used. The single trees are subsequently used to compute the lateral root reinforcement, the basal root reinforcement, and the vegetation weight. Both root reinforcement components are computed via a parameterisation of the equations, as used in Gehring et al. (2019). The vegetation weight is quantified by assuming a cone shape and a specific wood density.
All parameters are extracted for the HLs. Using the limit equilibrium approach (well described in Day 1997), a factor of safety (FoS) is computed for each HL. An HL is considered unstable if the FoS is <1. Sufficient spatial overlap of the HLs ensures that a fraction of unstable HLs can be computed for each point in a study area. This serves as a raster for relative landslide susceptibility.
A sensitivity analysis has been performed using three study areas in Switzerland. This identified soil depth, soil cohesion and root reinforcement as the primary factors influencing the correct prediction of shallow landslides. Validation was performed using the receiver operation curve (ROC) analysis. This method defines the accuracy of the model on a scale of 0.5 to 1.0, where 0.5 is no better than a random guess and 1.0 is a perfect prediction. SfM, with single tree detection, achieved an average accuracy of 0.84. Without single tree detection the accuracy was significantly lower.
Figure 2 is an example of a typical output from the case study in Eriz, Switzerland. In the next step, case studies from New Zealand will be chosen for validation and cost–benefit analysis of the bioengineering measures.
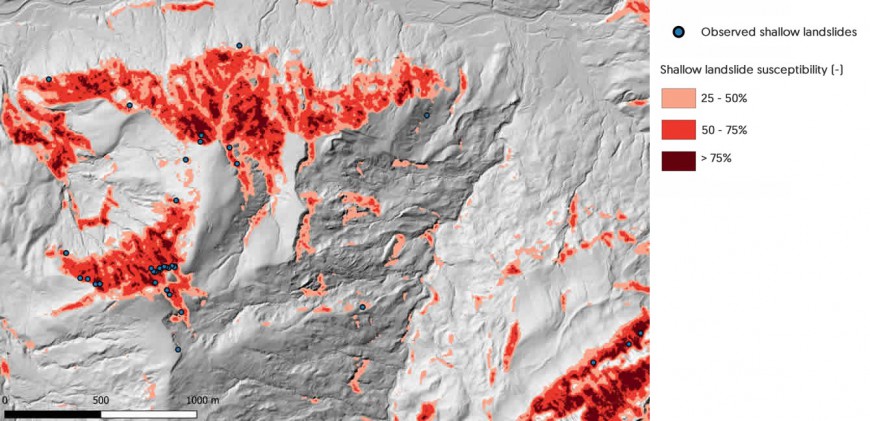
Figure 2. Example of the relative landslide susceptibility as computed by SlideforMap. This is for a mountainous test area in Switzerland and a precipitation intensity of 38 mm/h.
Poplar root fieldwork
Fieldwork on tree roots is important for quantifying root reinforcement in SlideforMap, so for 5 weeks in autumn 2019 fieldwork was conducted at the Ballantrae Farm near Woodville. The goal of the fieldwork was to quantify the root reinforcement poplar trees can add to stabilising a slope. The first part consisted of counting roots around selected poplar trees. Trenches were dug around four trees and the roots were counted. Figure 3 shows the results of the average distribution of poplar roots.
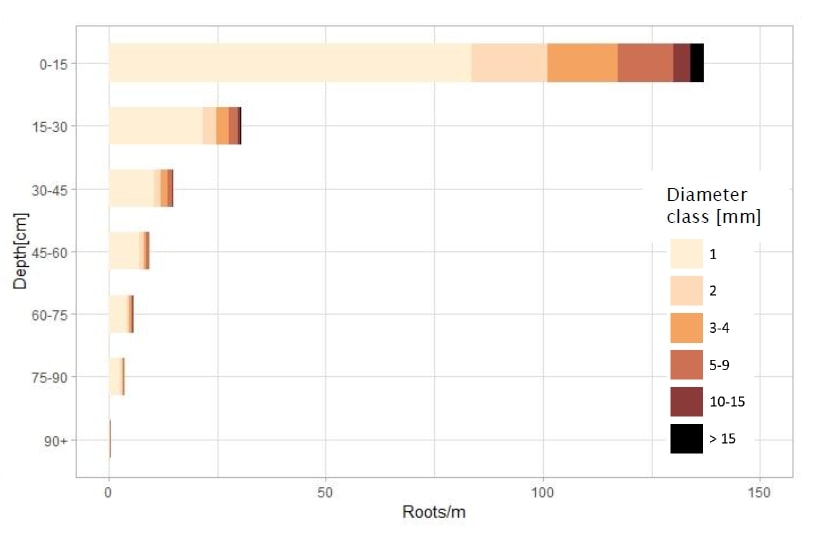
Figure 3. The average distribution of roots on a poplar trees for selected depth classes. A distinction is made for selected diameter classes of the roots.
The second part of the fieldwork involved using a pull-out test to find the tensile stress that roots can resist. This has been performed successfully 64 times on roots with a diameter between 5.7 and 44.1 mm. Fieldwork was carried out by students from HAFL (Bern University of Applied Sciences; School of Agricultural, Forest and Food Sciences, two of whom completed Bachelor’s projects (Ivo Gasparini and Julien Plaschy), with another embarking on a PhD programme (Feiko van Zadelhoff). Accounts of this work can be found in the previous STEC News.
From the fieldwork results, the Root Bundle Model (RBM) (Schwarz et al. 2013) is calibrated and used to calculate root reinforcement. The result is then used to calibrate the model to estimate lateral and basal root reinforcement as a function of tree species, tree dimension, and distance from tree stem.
The results of this calibration are shown in Figure 4. This approach is implemented in SlideforMAP to quantify the stabilising effect of roots for different scenarios of rainfall events and forest structure.
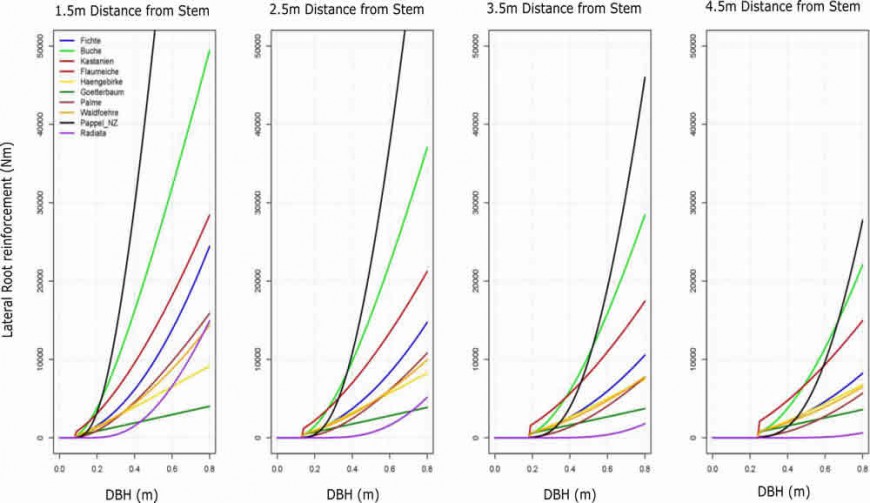
Figure 4. A comparison of the root reinforcement generated by our poplar trees and other tree species. The poplars are the black line. The y-axis gives the lateral root reinforcement in N/m. The x-axis gives the DBH in metres. Selected distance classes ar
A full overview of the fieldwork study site and the trees included can be found at https://fvzadelhoff.nl/Potree/nz_2/OurWebViewer.html.
In conclusion, we have proven that poplar trees have a stabilisation capacity that exceeds the mean of other well-known tree species. Radiata pine trees seem to perform less well.
References
Day RW 1997. State of the art: limit equilibrium and finite-element analysis of slopes. Journal of Geotechnical and Geoenvironmental Engineering 123(9): 894.
Gehring E, et al. 2019. Shallow landslide disposition in burnt European beech (Fagus Sylvatica L.) forests. Scientific Reports 9(1): 1–11.
Malamud B, Turcotte D, Guzzetti F, Reichenbach P 2004. Landslide inventories and their statistical properties. Earth Surface Processes and Landforms 29(6): 687–711.
Montgomery DR, Dietrich WE 1994. A physically based model for the topographic control on shallow landsliding. Water Resources Research 30(4): 1153–1171.
Schwarz M, Giadrossich F, Cohen D 2013. Modeling root reinforcement using a root-failure Weibull survival function. Hydrology & Earth System Sciences 17(11).
